| descartes-src (ソースパッケージ descartes-src-0.26.0.tar.gz) | 2012-09-09 20:57 |
| descartes-win (Windows用バイナリパッケージ descartes-win-0.26.0.zip) | 2012-09-09 20:52 |
| 会話キャラクター: ツンデレ アプリケーション (会話キャラ:ツンデレ v1.0 for Windows) | 2010-04-29 13:41 |
| 会話キャラクター: 2人の女の子 ダブルキャラクター (会話キャラクター 2人の女の子 ダブルキャラクター 1.0 for Windows) | 2011-10-02 22:23 |
| 会話キャラクター: Eliza風英語版 (会話キャラ:Eliza風英語版 v1.0 for Windows) | 2010-05-11 01:06 |
| 会話キャラクター: 猫耳メイド アプリケーション (会話キャラ:猫耳メイド v1.0 for Windows) | 2010-04-27 21:15 |
| 会話キャラクター: イライザ風日本語版 (会話キャラ:イライザ風日本語版 v1.0 for Windows) | 2010-04-30 21:53 |
| 経済指標表示プログラム for Windows (経済指標表示プログラム V1.0) | 2011-08-18 22:04 |
| ニュースヘッドライン表示プログラム (ニュースヘッドライン表示プログラム V1.0 for Windows) | 2011-08-16 12:31 |
| デカルト言語 example (デカルト言語の例題 example-0.7.0.zip) | 2009-03-01 19:47 |
| 電力状況表示プログラム for Windows (2011年夏版 全国電力供給状況表示プログラム V1.0) | 2011-08-15 13:25 |
ハノイの塔という有名な問題があります。
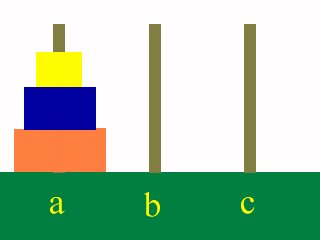
3本の棒が立っていて、一本の棒にn枚の円盤が大きさの順番に刺さっています
この円盤をaの位置からbの位置に次に示すようなルールに従って移動させなければなりません。
1. 動かせる円盤は、一度に一枚だけです。 2. 常に大きな円盤の上には小さな円盤しか乗せてはいけません。 3. a, b, c以外には円盤を置いてはいけません。
移動し終わると、すべての円盤がbの棒に刺さります。
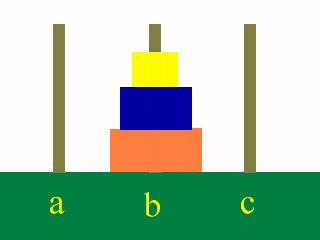
有名な問題なのでご存知の人も多いでしょう。 プログラムの例題として、いろいろなコンピュータ言語の例題として説明されることが多いものです。
この問題は、再帰的なプログラムで簡単に解くことができます。
1. n-1枚を、aからcへ移します。
移す方法は、本手順を再帰的に実行して行います。
2. aの残った最も大きい円盤を、bに移します。
これは、単純に1枚移すだけです。
3. cの棒から、さらに1枚残して、aに移します。
移す方法は、本手順を再帰的に実行して行います。
最初の手順では、以下のようになります。

次にcからaに一番下の円盤を残して移し、一番下の円盤はbに移します。
最後にaからbに移せば完了です。
このように処理を再帰的に繰り返して、円盤を移していきます。
---
デカルト言語のプログラム例として、prolog風の解き方と、デカルト言語固有の'|'(論理OR)を使った解き方 について以降で説明していきましょう。
<hanoi 1 #from #to _>
<print #from "->" #to>
;
<hanoi #n #from #to #tmp>
<let #n1 = #n - 1>
<hanoi #n1 #from #tmp #to>
<print #from "->" #to>
<hanoi #n1 #tmp #to #from>
;
? <hanoi 3 a b c>;
まず、最初の部分"<hanoi 1 #from #to _>"は、1枚だけ残った最大の円盤を#fromから#toに移す処理です。 再帰処理では、最終的に処理を終了する処理であり、これ以上は再帰的に述語を呼び出さない土台となる処理でもあります。
引数の"_"は、無名変数です。変数ですが定まった名前を持たずに、どんな引数の値ともパターンマッチするものです。
<hanoi 1 #from #to _>
<print #from "->" #to>
;
次の"<hanoi #n #from #to #tmp>"は、再帰処理の中心となる処理です。
n-1枚を、#fromから#tmpへ移し、その後#tmpの棒から、さらに1枚残して、#toに移します。 この処理は、nが1枚になるまで繰り返し、再帰的に呼ばれ続けていきます。 最後の1枚になったところで、上記の""<hanoi 1 #from #to _>"が呼ばれて復帰します。
<hanoi #n #from #to #tmp>
<let #n1 = #n - 1>
<hanoi #n1 #from #tmp #to>
<print #from "->" #to>
<hanoi #n1 #tmp #to #from>
;
"? <hanoi 3 a b c>;"の処理は、実際にハノイの塔の処理を呼び出すものです。 引数の3は、3枚の円盤で、ハノイの塔の問題を示しています。 この数字を大きくすると、それに対応した枚数で問題を解きます。
円盤の枚数が増えていくと、移動完了までの手数はどんどん増えていきます。 枚数と手数の関係については、自分で考えてみると面白いですよ。そちらのほうが難問かもしれません。
このハノイの塔の例題をprolog言語で記述すると以下のようになります。
hanoi(1, From, To, _) :-
write(From, "->", To), nl.
hanoi(N, From, To, Tmp> :-
N1 is N - 1,
hanoi(N1, From, Tmp, To),
write(From, "->", To), nl,
hanoi(N1, Tmp, To, From).
?- hanoi(3, "a", "b", "c").
文法的に異なる述語や構文は書き換えられていますが、論理的には、ほぼ同等なのがわかるでしょうか。
'|'(論理OR)を使った解き方について説明します。
デカルト言語では、prolog言語とは異なり、論理ORがプログラムの制御に使えます。
例えば、以下の場合
(処理1 | 処理2 | 処理3) 次の処理
処理1の実行がすべて成功すると、処理2と処理3は実行されず、「次の処理」が実行されます。
処理1の実行が失敗すると、処理2が実行され成功すると、処理3は実行されず、「次の処理」が実行されます。
処理1と処理2の実行が両方とも失敗すると、処理3が実行され成功すると、「次の処理」が実行されます。
処理1も処理2も処理3も失敗すると、次の処理は実行されず全体の実行が失敗します。
つまり、|で区切られた処理は、そのどれかが成功すれば、次の処理を実行する論理ORの役割を果たします。
では、'|'(論理OR)を使ったハノイの塔のソースを見ていきましょう。
<hanoi #n #from #to #tmp>
<is #n 1>
<print #from "->" #to>
|
<let #n1 = #n - 1>
<hanoi #n1 #from #tmp #to>
<print #from "->" #to>
<hanoi #n1 #tmp #to #from>
;
? <hanoi 3 a b c>;
「1. prolog風の解き方」と見比べてみてください。
<hanoi 1 #from #to _>がなくなっています。代わりに2つあったhanoi述語が1つに統合されています。
1つの述語に統合するために、'|'を使っています。
'|'の前の部分は、「1. prolog風の解き方」の最初の述語に対応する処理です。引数のパターンマッチを使っていたものを is述語による引数の判定に置き換えています。 is述語は、デカルトの組み込み述語であり、第一引数と第二引数が一致するか判定する述語です。
'|'の後の部分は、「1. prolog風の解き方」の2つ目の述語に対応する処理です。
論理的には、このように「1. prolog風の解き方」と同じ構造のプログラムをコンパクトに実現しています。
上記の'|'論路ORの構造を見て、どこかで見たような気がしませんか?
(述語1 述語2 | 述語3 )
例えばC言語でいえば、まるでif ~ else ~と同様な条件判定の制御構造に見えてこないでしょうか?
if (述語1) {
述語2
} else {
述語3
}
そっくりです。つまり、'|'論路ORは、まるでif文のように使えるのです。 厳密にいうと、述語は全部条件判定をしますので、下記がより正しい表現です。
if (述語1 && 述語2) {
} else if (述語3) {
}
また、複数の'|'を使うと、if ~ else if ~ else if ~のように使えます。
(述語1 述語2 | 述語3 述語4 | 述語5 述語6 )
これは、C言語のif文でいえば、このような制御構造です。
if (述語1 && 述語2) {
} else if (述語3 && 述語4) {
} else if (述語5 && 述語6) {
}
'|'論路ORは、いくつでも必要なだけ付けて繋いでいくことができますよ。
では、単純にelse節のないif文はどのようにすればよいでしょうか。
if (述語1 && 述語2) {
}
デカルト言語では、[]が使えます。 これは、本来は[]でくくられた処理は、省略可能であることを示すものです。
[ 述語1 述語2 ] 次の述語
これは、述語1が失敗しても、次の述語が実行されます。
述語1が成功すれば、述語2が実行され、その後に、次の述語が実行されます。
どうでしょう。 述語1が成功すれば、述語2が実行されるでしょう。 他の言語の、elseのないif文と同様なプログラムの制御が実行されるのです。
[PageInfo]
LastUpdate: 2009-11-14 22:56:40, ModifiedBy: hniwa
[License]
![]() Creative Commons 2.1 Attribution
Creative Commons 2.1 Attribution
[Permissions]
view:all, edit:login users, delete/config:login users